NCERT Solutions For Class 10 Maths Chapter 1 Exercise 1.2 in Hindi
Are you looking for free NCERT Solutions for Class 10 Maths Chapter 1, then you have come to the right place.
We will also try to take you towards that higher education which is best for you so that you can make your future bright for free. Here’s what you need to know.
❖ Can You Also Visit
यहाँ हम हिंदी में लाये है NCERT का पूरा हल कक्षा 10 गणित पुस्तक के अध्याय 1 वास्तविक संख्याएँ । हमारी यह पोस्ट उन छात्रों के लिए विशेष उपयोगी हैं जो हिंदी माध्यम से पढ़ाई कर रहे हैं।
NCERT Solutions For Class 10 Maths Chapter 1 का पूरा हल नीचे बहुत सरल भाषा में दिया गया है।
| कक्षा: | 10 |
| अध्याय: | 1 |
| नाम: | वास्तविक संख्याएँ |
| भाषा: | हिंदी |
| पुस्तक: | गणित |

Ex 1.2 Class 10 Question 1. निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution
(i) 140
उपरोक्त विधि के अनुसार अभाज्य गुणनखण्ड निकालते हैं।
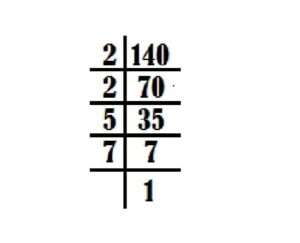
अतः संख्या 140 के अभाज्य गुणनखण्ड =2×2×5×7
Ans संख्या 140 के अभाज्य गुणनखण्ड =2²×5×7
(ii) 156
Solution
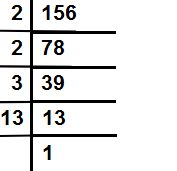
दी गई संख्या के अभाज्य गुणनखण्ड निकालते हैं।
अतः संख्या 156 के अभाज्य गुणनखण्ड =2×2×3×13
Ans संख्या 156 के अभाज्य गुणनखण्ड =2²×3×13
(iii) 3825
Solution
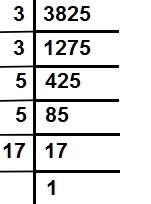
दी गई संख्या के अभाज्य गुणनखण्ड निकालते हैं।
अतः संख्या 3825 के अभाज्य गुणनखण्ड =3×3×5×5×17
Ans संख्या 3825 के अभाज्य गुणनखण्ड =3²×5²×17
(iv) 5005

उपरोक्त के अनुसार अभाज्य गुणनखण्ड निकालते हैं।
अतः संख्या 5005 के अभाज्य गुणनखण्ड =5×7×11×13
Ans संख्या 5005 के अभाज्य गुणनखण्ड =5×7×11×13
(v) 7429
Solution

उपरोक्त विधि के अनुसार –
अतः संख्या 7429 के अभाज्य गुणनखण्ड =17×19×23
Ans संख्या 7429 के अभाज्य गुणनखण्ड =17×19×23
Ex 1.2 Class 10 Question 2 .पूर्णाकों के निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि वो संख्याओं को गुणनफल = HCF x LCM है।
(i) 26 और 91
(ii) 510 और 92
(iii) 336 और 54
(i) 26 और 91
Solution
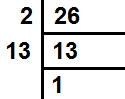
26 के गुणनखण्ड =2×13
और
91
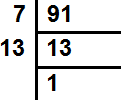
91 के गुणनखण्ड = 7× 13
किन्हीं दो संख्याओ का सार्व गुणनखण्ड ही उनका H.C.F होता है। अतः 26 और 91 का H.C.F = 13
किन्हीं दो संख्याओ का सार्व गुणनखण्ड तथा शेष गुणन खण्ड ही उनका L.C. M होता है।
अतः 26 और 91 का L.C. M = 2×7×13
=182
सूत्र
दो संख्याओ का गुणनफल = H.C.F×L.C.M
N1 ×N2= H.C.F×L.C.M
26×91= 13×182
2366 = 2366
यही सिद्ध करना था।
(ii) 510 और 92
Solution
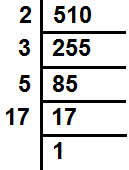
510 के गुणनखण्ड = 2×3×5×17
और
92
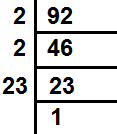
92 के गुणनखण्ड =2×2×23
किन्हीं दो संख्याओ का सार्व गुणनखण्ड ही उनका H.C.F होता है।
अतः 510 और 92 का H.C.F = 2
किन्हीं दो संख्याओ का सार्व गुणनखण्ड तथा शेष गुणन खण्ड ही उनका L.C. M होता है।
अतः 510 और 92 का L.C. M = 2×2×3×5×17×23
= 60×17×23
=1020×23
=23460
L.C.M = 23460
सूत्र
दो संख्याओ का गुणनफल = H.C.F×L.C.M
N1 ×N2= H.C.F×L.C.M
510×92=2×23460
46920 = 46920
Do not forget connect with us@go2math.com
यही सिद्ध करना था।
(iii) 336 और 54
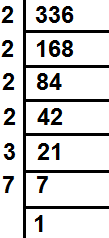
336 के गुणनखण्ड = 2×2×2×2×3×7
और 54
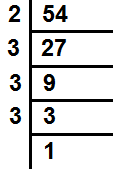
54 के गुणनखण्ड = 2×3×3×3
किन्हीं दो संख्याओ का सार्व गुणनखण्ड ही उनका म. स. (H.C.F) होता है।
अतः 336 और 54 का म. स. (H.C.F) = 6
किन्हीं दो संख्याओ का सार्व गुणनखण्ड तथा शेष गुणन खण्ड ही उनका L.C. M होता है।
अतः 336 और 54 का ल.स.(L.C. M) = 2×2×2×2×3×3× 3×7
= 16×27×7
=16×189
=3024
सूत्र
दो संख्याओ का गुणनफल = H.C.F×L.C.M
N1 ×N2= H.C.F×L.C.M
336×54= 6×3024
18144 = 18144
Like and share @go2math.com
यही सिद्ध करना था।
Ex 1.2 Class 10 Question.3 अभाज्य गुणनखण्डन विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए।
(i) 12, 15 और 21
(ii) 17, 23 और 29
(iii) 8, 9 और 25
(ii) 17, 23 और 29
(iii) 8, 9 और 25
(i) 12, 15 और 21
Solution
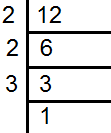
उपरोक्त विधि को ही अभाज्य गुणन खण्ड विधि कहते हैं।
इस विधि के अनुसार –
12 के अभाज्य गुणन खण्ड =2×2×3
15 के लिए

15 के अभाज्य गुणनखण्ड = 3×5
21 के लिए
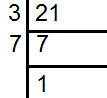
21 के अभाज्य गुणन खण्ड =3×7
H.C.F(म. स.)= सार्व गुणनखण्ड
12, 15 और 21 का H.C.F(म. स.) 3 होगा।
L.C.M(ल. स.) =2×2×3×5×7
12, 15 और 21 का L.C.M(ल. स.) 420 होगा।
(ii) 17, 23 और 29
Solution
17 के अभाज्य गुणन खण्ड निकालने पर
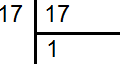
17 के अभाज्य गुणन खण्ड=17×1
23 के लिए
23 के अभाज्य गुणन खण्ड निकालने पर
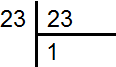
23 के अभाज्य गुणन खण्ड =23×1
29 के लिए
29 के अभाज्य गुणन खण्ड निकालने पर
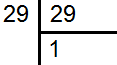
29 के अभाज्य गुणन खण्ड =29×1
H.C.F(म. स.)= सार्व गुणनखण्ड
=1
17, 23और 29 का H.C.F(म. स.) 1होगा।
L.C.M(ल. स.) =17×23×29
17, 23 और 29 का L.C.M(ल. स.) 11339 होगा।
(iii) 8, 9 और 25
Solution
8 के लिए
8 के अभाज्य गुणन खण्ड निकालने
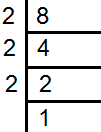
8 के अभाज्य गुणन खण्ड =2×2×2×1
9 के लिए
9 के अभाज्य गुणन खण्ड निकालने
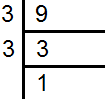
9 के अभाज्य गुणन खण्ड =3×3×1
25 के लिए
25 के अभाज्य गुणन खण्ड निकालने
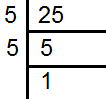
25 के अभाज्य गुणन खण्ड =5×5×1
H.C.F(म. स.)= सार्व गुणनखण्ड
=1
8, 9 और 25 का H.C.F(म. स.) 1 होगा।
L.C.M(ल. स.) =2×2×2×3×3×5×5
=8×9×25
=200×9
=1800
8, 9 और 25 का L.C.M(ल. स.) 1800 होगा।
Ex 1.2 Class 10 Question.4 HCF (306, 657) = 9 दिया है। LCM (306, 657) ज्ञात कीजिए।
Solution
सूत्र
दो संख्याओ का गुणनफल = H.C.F×L.C.M
N1 ×N2= H.C.F×L.C.M
306×657= 9×L.C.M
L.C.M= 306×657
9
= 34×657
=22338
L.C.M (306, 657) 22338 होगा।
Ex 1.2 Class 10 Question.5 जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या 6n अंक 0 पर समाप्त हो सकती है।
Solution
यदि कोई संख्या 0 पर समाप्त होती है तो वह 10 से अवश्य विभाज्य होगी।
10 के अभाज्य गुणन खण्ड=2×5
अर्थात तो वह संख्या 2, 5 से भी अवश्य विभाज्य होगी।
6ⁿ के अभाज्य गुणनखंड = (2×3)ⁿ
संख्या 0 पर समाप्त हो इसके लिए उस संख्या के अभाज्य गुणन (2×5)ⁿ के रूप में होने चाहिए।
अतः 6ⁿ के अभाज्य गुणनखंड (2×5)ⁿ के रूप में नहीं है अर्थात् यह 5 से विभाज्य नहीं होगा।
इसीलिए 6ⁿ, 0 पर समाप्त नहीं होगी।
इसी की जांच करनी थी।
Ex 1.2 Class 10 Question.6 व्याख्या कीजिए कि 7 x 11 x 13 + 13 और 7 × 6 x 5 x 4 x 3 x 2 x 1+ 5 भाज्य संख्याएँ क्यों हैं।
Solution
Composite number👉 वे सभी प्राकृत संख्याएँ जो अपने आप ,1 के अलावा भी अन्य किसी संख्या से पूरा-पूरा विभाजित हो जाती है उसे हम भाज्य संख्या (composite number) कहते है।
माना X= 7×11×13 + 13 और
Y= 7×6×5×4×3×2×1+ 5
X= 7×11×13 + 13
उपर्युक्त में से 13 कॉमन लेने पर
X=13(7×11+1)
X=13×78
X=13×6×13
X=13×2×3×13
X=1014
अतः 7×11×13 + 13 यह एक भाज्य संख्या हैं। क्योंकि इसके एक से अधिक गुणन खण्ड हैं।
इसी तरह,
Y= 7×6×5×4×3×2×1+ 5
उपर्युक्त में से 5 कॉमन लेने पर
Y= 5(7×6×4×3×2×1+ 1)
Y= 5(7×6×24+1)
Y=5(1008+1)
Y=5×1009
Y=5045
अतः 7×6×5×4×3×2×1+ 5 यह एक भाज्य संख्या हैं। क्योंकि इसके एक से अधिक गुणन खण्ड हैं।
Ex1.2 Class 10 Question.7 किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारंभिक स्थान पर मिलेंगे?
Solution
उपरोक्त प्रश्न में L.C.M ल. स. निकालने से वह समय ज्ञात हो जायेगा जहां पर वे पुनः प्रारंभिक स्थान पर मिलेंगे
प्रश्न में दिया है –
मैदान का एक चक्कर लगाने में सोनिया को लगा समय= 18 मिनट
मैदान का एक चक्कर लगाने में रवि को लगा समय= 12 मिनट
वह समय जहां पर वे पुनः प्रारंभिक स्थान पर मिलेंगे =(12,18) का L.C.M ल. स.
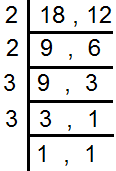
12 व 18 का L.C.M ल. स. = 2×2×3×3
=4×9
=36
अतः वह समय 36 मिनट है जब सोनिया और रवि पुनः प्रारंभिक स्थान पर मिलेंगे।
❖ Can You Also Visit
❖ NCERT Solutions For Class 10 Maths Chapter 1 ex1.3 in Hindi
❖ NCERT Solutions For Class 10 Maths Chapter 1 ex1.4 in Hindi
Maybe also Best For Exam